 |
 |
 |

制御の基礎で基本は微積分だと話しました。
1次の微積分ならそのまま計算しても容易に解けます。
しかし系が複雑になって高次になってくると微積分方程式を解くのは容易ではなくなります。
昔、計算尺というのがありましたね。電卓がない時代に乗除算を計算するのが容易ではなかったので log変換して加減算して exp (逆log) 変換すると乗除算が容易にできるというのが計算尺の原理です。
微積分は時間軸を周波数軸に変換すると積分が乗算、微分が除算になります。このような変換にはラプラス変換やフーリエ変換があります。
とりあえずそういうものだと思い、ラプラス変換やフーリエ変換とは何かを深く考えないのが制御設計のコツです。
ラプラス変換では、積分はsをかける、微分はsで割る、
フーリエ変換では、積分はjωをかける、微分はjωで割るとなります。
そうすることによって時間tの関数がラプラス変換ならsの関数になります。
ラプラス変換とフーリエ変換の違いはsかjωかだけなので、とりあえずsで計算しておいて周波数にしたいときは s=jω と置き換えます。
それからラプラス変換して制御設計することはブロック図を使用します。
ニュートンの運動方程式は f=ma ですが、a および f を時間の関数とすると f(t)=ma(t) です。
v(t)=∫a(t) dt=1/m ∫f(t)dt
これをラプラス変換で表すと、積分→sを掛けるとなるので、
V(s)=s/m F(s) となります。
オープンループ系では、力から速度への伝達のブロック図は第1図のようになります。
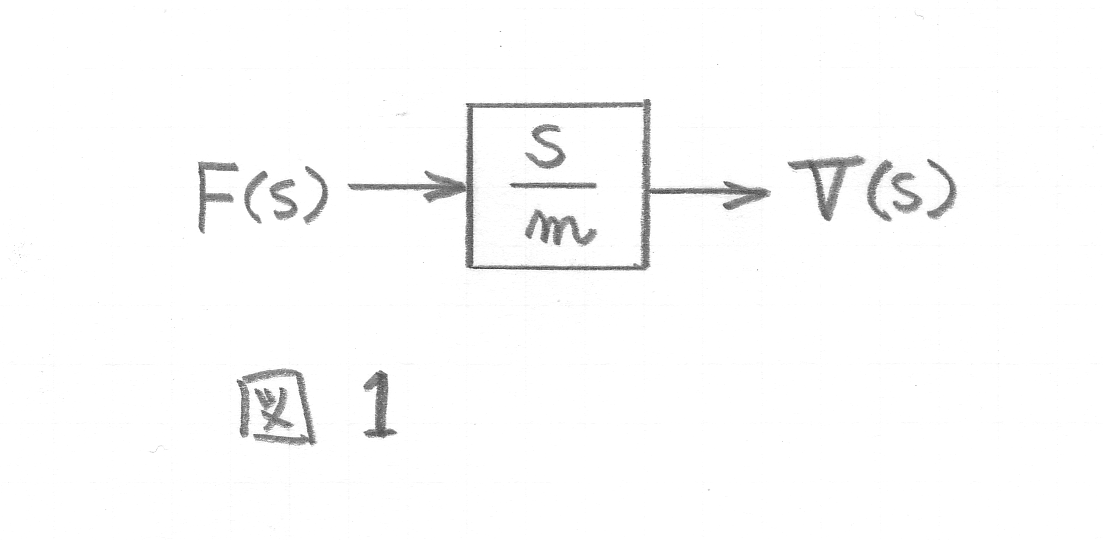
次に速度制御を掛けたフィードバック制御を考えてみます。
速度を検出して電圧に変換する -- 速度検出ゲインKv(速度→電圧)
基準電圧Esと比較して誤差を増幅する -- アンプゲインA(電圧→電圧)
アンプ出力をアクチュエータなどで力に変換する -- 力定数Kf(電圧→力)
質量mにより力の積分が速度になる -- s/m(F(s)→V(s))
質量には外乱FL(s) が加わる。
と考えるとブロック図は図2になります。
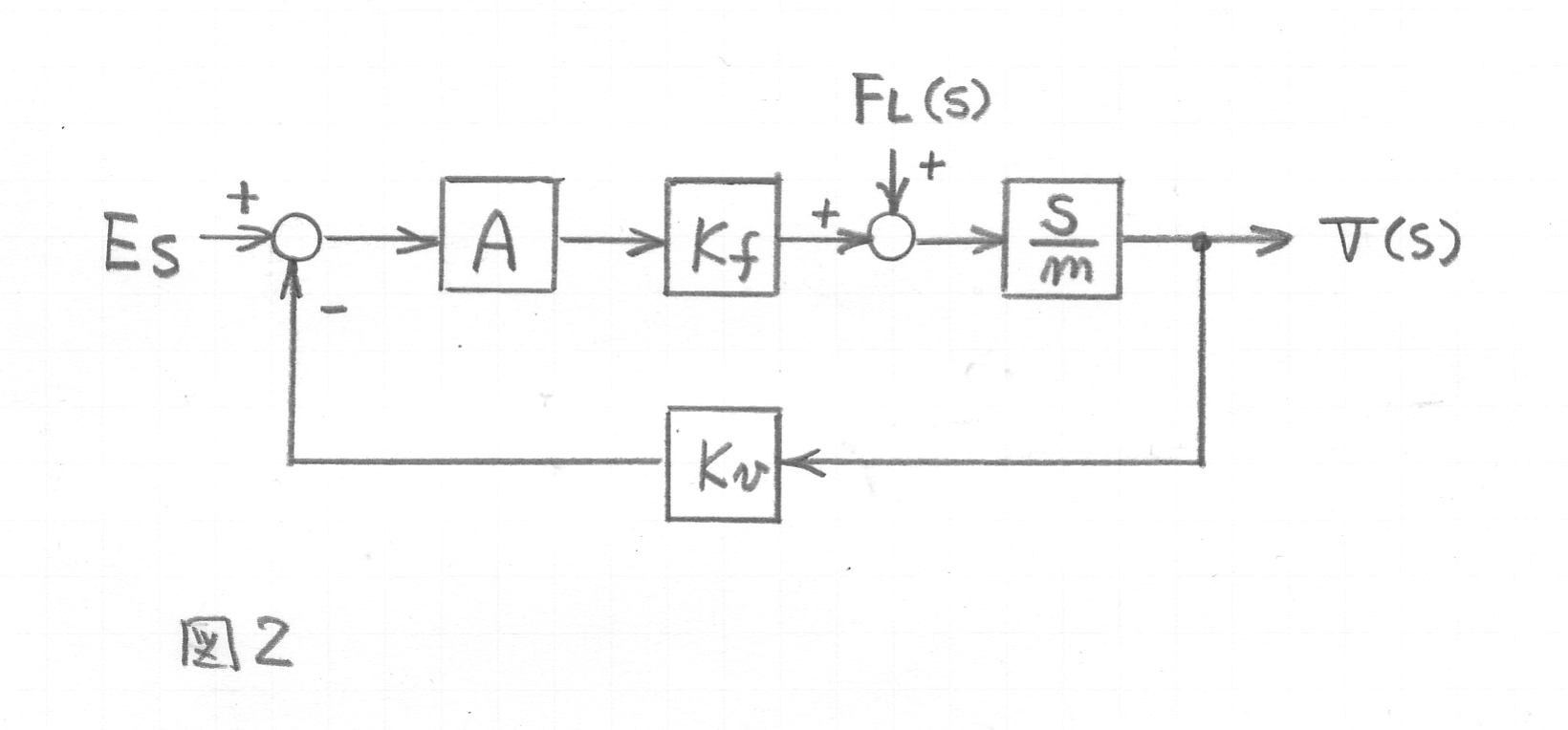
考えやすくするために
Es=0、K=Kv×A×Kf と置くとブロック図は図3になります。
外乱から速度への伝達は図3の G(s) になります。
この式はカットオフ周波数 f0=m/(2πK) のHPFの特性と同じです。
低域の伝達はKに反比例しますのでゲインが大きくなると外乱の影響を受けにくくなることがわかります。
しかし高域のゲインは変わりませんので、カットオフ周波数以上の周波数を制御することはできません。

このような積分要素が1つの制御系を1次遅れ系と言います。
|
|
|
 |
 |
半導体回路・電子回路・電子機器設計のご用命は 有限会社安田電子設計事務所へ!! |
 |
 |
Home
技術紹介
サービス案内
会社概要
お問い合わせ
|
 |
 |
 |
 |
 |
Copyright(C) 2010 Yasuda Electronics Design Office All Rights Reserved. |
 |

